4화. 양자 컴퓨터의 활용 가능성과 보안 암호에 대한 위협

○ 미국의 저명한 물리학자인 리차드 파인만에 의해 양자 컴퓨터의 개념이 제시된 후, 양자 컴퓨터가 어떤 문제를 빨리 풀 수 있는지에 대한 연구와 함께 다양한 활용 가능성이 논의 → 약 60개 정도의 수학 문제에서 양자 컴퓨터가 기존의 컴퓨터보다 문제를 빠르게 푼다고 알려짐¹¹

• 예를 들면, 복잡한 확률 문제를 계산하는 화학 분야에서 신약이나 신소재를 개발하거나, 물류나 교통 분야에서 시작점에서 목적지를 찾아가는 최소/최단 경로 찾기, 금융 분야에서의 포트폴리오 최적화, 옵션가격 결정 모델링, 암호 해독 등에서 활용이 기대

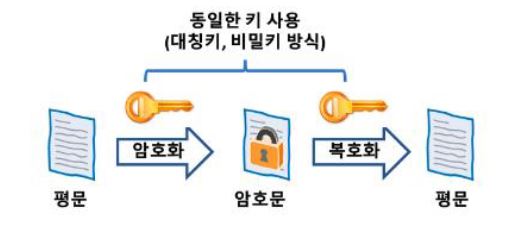
○ 특히, 60개의 수학 문제 중 하나가 소인수 분해¹² 문제를 풀 수 있는 알고리즘이라 화제가 됨

○ 2021년 5월, 포브스지는 90% 이상의 암호화된 인터넷 트래픽이 RSA 알고리즘을 사용한다고 발표¹⁴. 만약 양자 컴퓨터가 발전하여 이러한 암호를 쉽게 풀 수 있다면, 기존의 인터넷을 오가는 수 많은 정보들이 쉽게 해킹되어 이메일 내용이 공개되고, 금융 서비스가 마비되는 등 암호체계가 무력화 되지 않을까 하는 우려가 커진 것

○ RSA 알고리즘은 비대칭키(공개키) 기반의 암호 알고리즘으로 소인수 분해가 어렵다는 데 기반

• 암호 방식은 암호를 걸어주는 키와 암호를 푸는 키를 동일하게 쓰는 대칭키 방식과 서로 다른 키를 사용하는 비대칭키 방식으로 구분되며, 비대칭키는 공개키라고도 부름
  
  - 대칭키 방식은 동일한 키를 사용해서 암호화 및 복호화를 진행되므로 빠르다는 장점이 있지만, 키를 상호간에 전달할 때 키가 탈취될 수 있는 키 배송의 문제가 발생. 또한, 이용자가 증가할수록 전부 따로 따로 키를 교환해야 하므로 관리 이슈가 발생
  
  - 비대칭키(공개키) 방식은 대칭키 방식의 문제를 해결하기 위해 나온 방식으로 서로 다른 키를 사용. 공개키는 모든 사람이 접근 가능하지만, 개인키는 각 사용자만이 가지고 있으며, 개인키를 가진 사람만이 암호를 풀 수 있어 인증 기능도 제공한다는 장점

• RSA 암호 알고리즘은 비대칭키 방식으로, 이러한 암호 체계에서는 불특정 다수에게 공개되는 공개키를 이용해 비밀키를 알아내거나 복호화를 하기 어렵게 만드는 것이 중요
  
  - 소인수 분해는 두 소수를 곱해서 큰 수를 만드는 것은 쉽지만, 그 반대의 계산은 어려운 비대칭성을 활용 → 공개키로 두 개의 소수의 곱을 사용
  
  - 예를 들어, 21은 쉽게 3x7로 누구나 쉽게 소인수 분해를 할 수 있음. 323의 경우 17x19로 조금은 시간이 걸리더라도 소인수 분해가 가능하겠지만, 702,340,952,147의 경우 컴퓨터가 없이는 대단히 어려울 것

• 기존의 컴퓨터로 이러한 소인수 분해 문제를 풀기 위해서는 2의 배수인지, 3의 배수인지, 5의 배수인지 숫자를 하나씩 늘려가면서 실제 나눗셈을 해봐야 함
  
  - 100이하의 소수는 25개이고, 1,000이하의 소수는 168개, 10,000이하의 소수는 1,229개, 100,000이하의 소수는 9,592개로 자릿수가 하나 늘어날 때마다 해야할 계산량이 대략적으로 10배씩 증가함을 확인할 수 있음¹⁵
  
  - RSA-2048 알고리즘의 공개키는 617자리의 수로, 인수분해를 위해 소수를 하나씩 대입해보는 기존 컴퓨터의 계산 방식으로는 300조년 이상의 시간이 필요¹⁶
  
  (RSA-2048 공개키 예시:
  25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357)

○ 1994년 피터 쇼어에 의해 고안된 소인수 분해 알고리즘은 기존의 컴퓨터의 계산 방식과는 달리 합리적인 시간내에 소인수 분해 문제를 풀 수 있다는 것을 이론적으로 증명

• 앞서 살펴본 양자 컴퓨터를 활용한다면 큐비트가 늘어날수록, 표현할 수 있는 경우의 수가 2배씩 증가하므로 큐비트의 수를 충분히 늘리면 동시에 표현할 수 있는 경우의 수가 많아져, 쇼어 알고리즘을 이용하면 합리적인 시간내에 소인수 분해 문제를 풀 수 있다는 것

• 2021년, 구글은 ‘RSA-2048 정수를 소인수 분해 하는데 오류가 있는 2,000만 큐비트의 양자 컴퓨터로 8시간이 필요하다는 논문을 발표¹⁷ (실제로 이러한 양자 컴퓨터가 없으므로, 오류율을 1천분의 1, 한 번 계산하는데 0.001초가 걸린다고 가정)
  
  - 연구자마다 어느 정도의 큐비트가 필요한지 차이가 있으나 대략적으로 오류가 있는 수백만 큐비트의 양자 컴퓨터가 있으면 합리적인 시간내 RSA 알고리즘을 풀 수 있다고 알려져 있음¹⁸

○ 하지만, 대다수 전문가들은 근 시일내 암호 체계가 붕괴될 위험이 크지는 않을 것으로 예상¹⁹

• 쇼어 알고리즘이 제안된 지 20년이 넘게 지났지만, 아직은 실험으로 소인수 분해에 성공한 최대의 수가 15=3x5(2001년), 21=3x7(2012년)에 불과²⁰하며, 이 결과도 알고리즘이 작동하기 유리한 방식으로 진행되어 완벽하게 실험적으로 증명된 것은 아니라는 반론이 있으며,

• 이상적인 양자 컴퓨터에서는 효율적인 성능을 보여줄 수 있겠지만, 양자 컴퓨터를 만드는 데 기술적 어려움이 많아 당장 모든 암호가 무력화되지는 않을 것이라는 게 전문가들의 중론²¹
  
  - 구글의 시카모어의 경우 53큐비트를 가진 양자 컴퓨터이지만, 실제로는 ‘난수’를 생성하는 알고리즘 문제를 풀며 기존 슈퍼 컴퓨터보다 우수한 성능을 보인 사례에 불과하여, 소인수 분해를 풀기에는 큐비트를 더 늘리고, 오류를 낮춰야 하는 등 한계 존재²²
  

• 아울러 기존의 암호 알고리즘들도 양자 컴퓨터에 선제적으로 대응하기 위해 더욱 자릿수를 늘리거나, 인수분해 기반이 아닌 다른 어려운 수학 문제에 기반한 알고리즘을 연구하고, 양자의 특성을 활용한 암호통신을 개발하는 등 양자 컴퓨터의 운영이 시작되더라도 앞으로 적어도 20년간은 기존의 암호화 시스템을 지킬 수 있을 것이라는 의견²³도 존재
  
  - 양자 컴퓨터도 풀기 어려운 수학적 알고리즘 기반의 암호 체계인 양자내성암호(PQC: Post Quantum Cr yptography)에 대한 연구나 광자를 이용하여 중간에 탈취/복제를 시도하는 순간 암호의 형태와 내용을 바꾸어 해킹을 원천 봉쇄하는 양자암호통신기술 등도 개발중